त्रिभुज – परिभाषा, प्रकार, परिमाप, क्षेत्रफल

त्रिभुज के बारे में सम्पूर्ण जानकारी जैसे की परिभाषा, परिमाप, प्रकार, क्षेत्रफल, इत्यादि इस लेख में बताई गयी है। इसमें त्रिभुज को सरल भाषा में तथा सभी जानकारी विस्तार से है।

त्रिभुज की परिभाषा

त्रिभुज एक तीन भुजाओ से घिरी बंद आकृति होती है। इसमें तीन कोण होते है। इन तीनो कोनो का जोड़ 180 डिग्री होता है।

याद रखें –

• एक त्रिभुज में तीन भुजाएं एवं तीन कोण होते है।
• तीनो कोणों का जोड़ हमेशा 180 होता है।

त्रिभुज के प्रकार

त्रिभुज के प्रकार को दो तरह से वर्गीकृत किया गया है –

1. भुजाओ के आधार पर त्रिभुज के प्रकार
   • समबाहु त्रिभुज – तीनो भुजाएं समान होती है। प्रत्येक कोण 60^o का होता है।
   • समद्विबाहु त्रिभुज -दो भुजाएं तथा तीसरी भुजा पर बने कोण समान होते है।
   • विषमबाहु त्रिभुज – कोई भी भुजा समान नही होती है।
2. कोणों के आधार पर त्रिभुज के प्रकार
   • समकोण त्रिभुज – एक कोण 90 डिग्री का होता है।
   • न्यूनकोण त्रिभुज – सभी कोण न्यूनकोण ( < 90^o ) होते है।
   • अधिक कोण त्रिभुज – एक कोण अधिक कोण ( > 90^o ) होता है।

त्रिभुज के प्रकार के बारे में और पड़े – त्रिभुज के प्रकार

त्रिभुज का परिमाप

परिमाप किसी आकृति के चारो और की सीमाओं का योग होता है। परिमाप को परिधि भी कहते है।

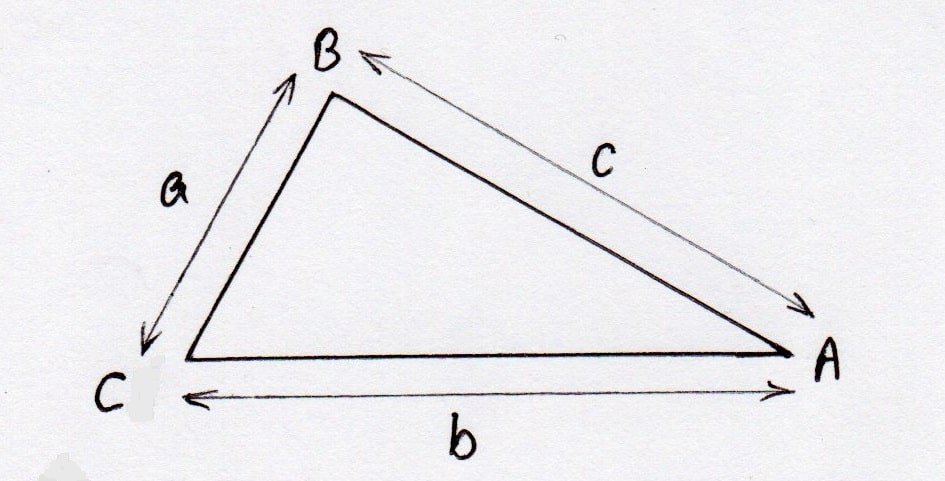
त्रिभुज का परिमाप उसकी तीनो भुजाओ का योग होता है। इसलिए त्रिभुज के परिमाप का सूत्र उसकी तीनो भुजाओ का जोड़ (a+b+c) होगा।

त्रिभुज का परिमाप = a+b+c

त्रिभुज का अर्द्ध परिमाप (s) = (a+b+c)/2

Read More – त्रिभुज का परिमाप विस्तार से

त्रिभुज का क्षेत्रफल

क्षेत्रफल किसी आकृति द्वारा घेरी गयी जगह को कहते है।

त्रिभुज का क्षेत्रफल विभिन्न प्रकारो से ज्ञात किया जा सकता है। अलग अलग प्रकार के त्रिभुज के लिए अलग क्षेत्रफल के सूत्र लगाये जाते है ताकि क्षेत्रफल आसानी से ज्ञात किया जा सके।

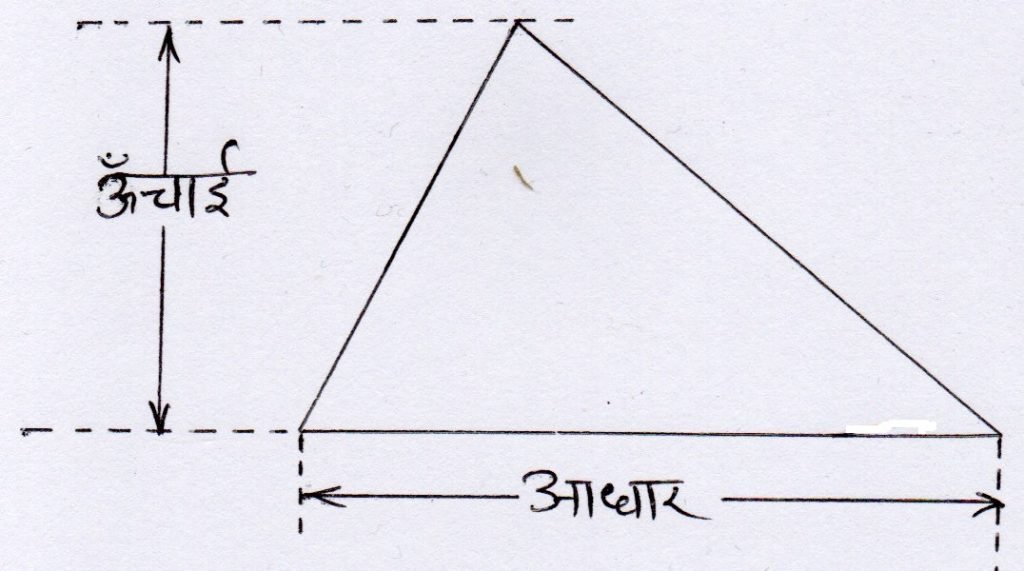
त्रिभुज का क्षेत्रफल उसके आधार तथा ऊंचाई के गुणन का आधा होता है।

अर्थात त्रिभुज के क्षेत्रफल का सूत्र –

त्रिभुज के क्षेत्रफल = ¹/₂ X आधार X ऊंचाई

अगर त्रिभुज समकोण त्रिभुज है तो उसका लम्ब ही उसकी ऊंचाई होती है।

अन्य प्रकार के त्रिभुज जैसे समबाहु, समद्विबाहु, विषमबाहु, इत्यादि के क्षेत्रफल के लिए यहाँ विस्तार से पड़े –

सभी प्रकार के त्रिभुज का क्षेत्रफल