त्रिभुज का परिमाप और उसके विभिन्न सूत्र (Formula), आज हम इस आलेख में सीखेंगे। इसमें हम त्रिभुज का परिमाप उदाहरण सहित विस्तार से जानेंगे।
त्रिभुज से सम्बंधित अन्य आलेख पढ़े –
- त्रिभुज – परिभाषा, प्रकार, परिमाप, क्षेत्रफल संक्षिप्त में
- त्रिभुज के प्रकार
- त्रिभुज का क्षेत्रफल : सूत्र स्पष्टीकरण और उदाहरण
त्रिभुज का परिमाप क्या होता है ?
किसी भी आकृति का परिमाप उस आकृति की सीमा रेखा (Boundary) की लम्बाई होता है। परिमाप को परिधि भी कहते है।
त्रिभुज एक बहुभुज (Polygon) है जिसकी तीन भुजाएं होती है। इसलिए त्रिभुज का परिमाप उसकी तीनो भुजाओं का योग होता है।
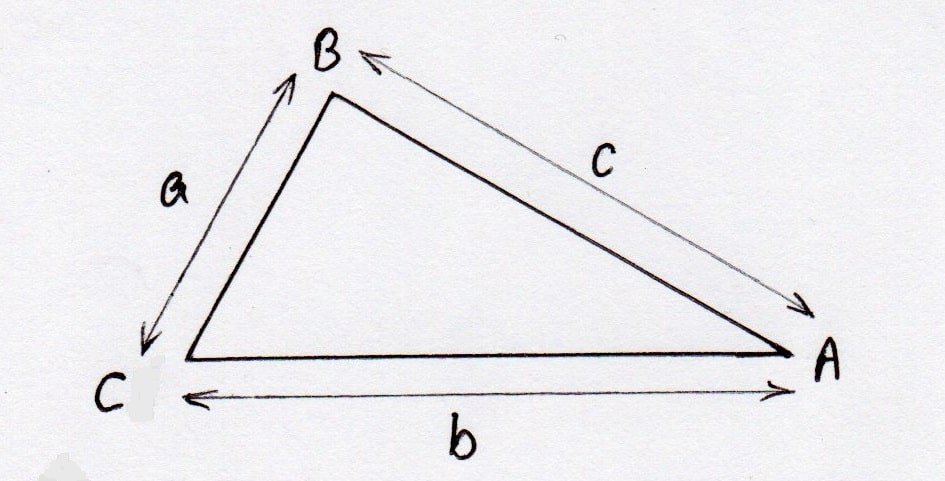
ऊपर दिए गयी त्रिभुज की आकृति में उसकी तीन भुजाये a, b तथा c, उसकी सीमा रेखा है इसलिए –
त्रिभुज का परिमाप का सूत्र = a+b+c
सभी त्रिभुज, चाहे वो किसी भी प्रकार का हो, का परिमाप इसी सूत्र से ज्ञात किया जाता है।
लेकिन हमारी आसानी के लिए विभिन्न प्रकार के त्रिभुजों का परिमाप, उनकी विशेषता के हिसाब से सरल रूप में भी लिखा जा सकता है।
आइये देखते है –
समबाहु त्रिभुज का परिमाप
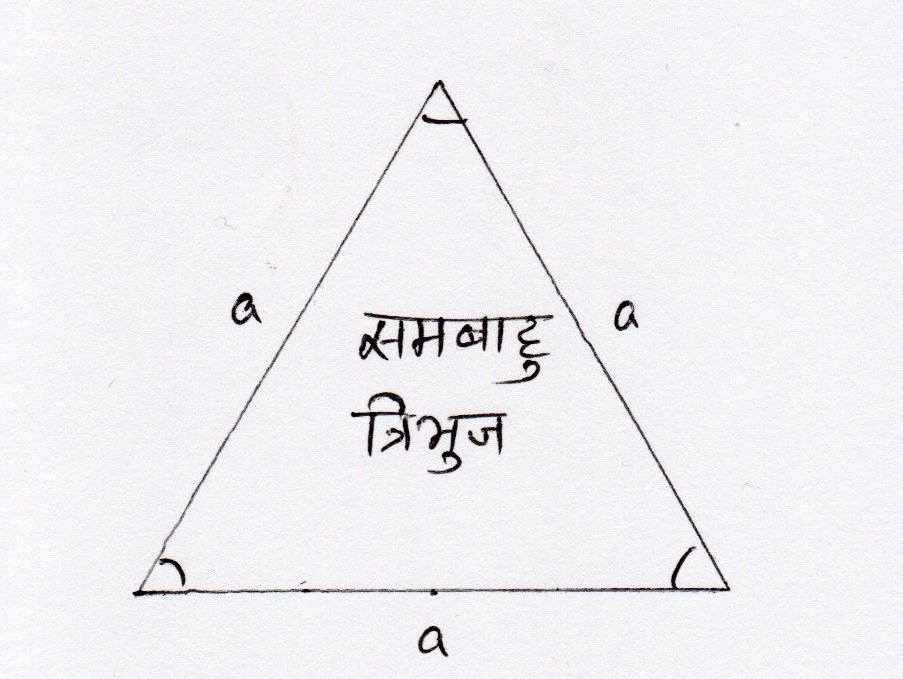
समबाहु त्रिभुज का परिमाप का सूत्र और भी आसान होता है। चूँकि समबाहु त्रिभुज की तीनो भुजाएं समान होती है, इसलिए –
समबाहु त्रिभुज का परिमाप का सूत्र = 3 x भुजा
सूत्र स्पष्टीकरण – त्रिभुज का परिमाप = a+b+c समबाहु त्रिभुज में a=b=c होता है, इसलिए Sambahu tribhuj ka Parimap = a+a+a = 3 x a; जहाँ a समबाहु त्रिभुज की भुजा की लम्बाई है।
समद्विबाहु त्रिभुज का परिमाप
हम जानते है की समद्विबाहु त्रिभुज में दो भुजाएं समान लम्बाई की होती है। इसलिए –
समद्विबाहु त्रिभुज का परिमाप = 2a+c
सूत्र स्पष्टीकरण – त्रिभुज का परिमाप = a+b+c समद्विबाहु त्रिभुज में माना a=b है, इसलिए samdibahu tribhuj ka Parimap = a+a+c = 2a+c; जहाँ a, b, c समद्विबाहु त्रिभुज की भुजा की लम्बाई है।
NOTE:- ध्यान रहें की इस तरह सभी सूत्र याद करने की जरुरत नहीं है बल्कि सूत्रों को समझकर पढ़े तथा उसके पीछे की धारणा (Concept) को समझकर याद रखे। जैसे की इस आलेख में सबसे महत्वपूर्ण त्रिभुज के परिमाप के बारे में जानना है, ना की समबाहु त्रिभुज, विषमबाहु और समद्विबाहु त्रिभुज के परिमाप। क्योंकि अगर हमें त्रिभुज के प्रकार एवं विशेषताएं पता होंगी तो सभी के परिमाप बहुत ही सरलता से ज्ञात किये जा सकते है। इसके लिए सूत्रों को रटने की जरुरत नहीं है।